Digital Filtering: Aliasing
The examples below can be found in Control/Filter/Filter_Examples.m in GNCTools.
One of the most important (practical) concepts to be familiar with in signal processing is aliasing, which can lead to some pretty confusing results if not appreciated, and accounted for. While the fix is generally simple (add an anti-aliasing analog low pass filter or oversampling with a digital low pass filter), it is helpful to understand what aliasing looks like so you can spot it in future.
Aliasing Examples
To illustrate the effects of aliasing, consider the following examples. For these examples, we'll use the following "continuous" (i.e. generated with a small enough time interval to be effectively continuous, rather than discrete) 10Hz sine wave, for example pretending it is the analog input to an ADC:
Fs = 1e3; % Assume 1kHz fast enough
Fsine = 10;
tFinal = 2;
t = 0:(1/Fs):tFinal;
u = sin(Fsine*2*pi*t); % remember w [rad/s] = 2*pi*f [Hz]
Sampled At The Maximum Frequency Contained
Let's see what would happen if we sampled the input sine wave signal at the same frequency as the maximum frequency contained in the signal (10Hz):
Fn = Fsine * 1;
tn = (0:(1/Fn):tFinal);
un = interp1(t,u,tn);
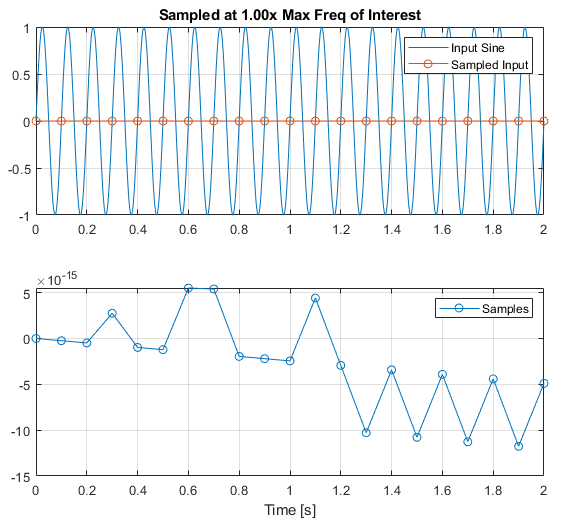
and look at that - our sampled output would return all 0! Now obviously if there was noise in the signal, we would see some of that, but fundamentally we have missed the entire sine wave in our sampling. If we happened to start sampling the input not at the beginning of a cycle:
Fn = Fsine * 1;
tn = (0:(1/Fn):tFinal) + 0.01;
un = interp1(t,u,tn);
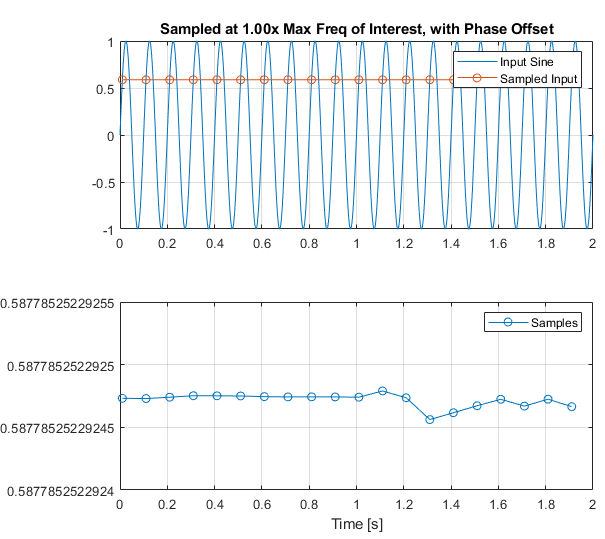
we would get a constant value again, but offset based on the phase offset of our sampling to the original signal. Effectively, due to aliasing, we could say a piece of equipment is dead (not producing any output, i.e. 0V), when in fact it is, just at a higher frequency than we can measure correctly! Or that there is no oscillation at all in a signal, and just a constant, when again there is.
Sampled Near The Maximum Frequency Contained
Let's repeat, but at frequencies very close to the maximum frequency present in the signal (i.e. near to 10Hz):
Fn = Fsine * 1.05;
tn = (0:(1/Fn):tFinal);
un = interp1(t,u,tn);
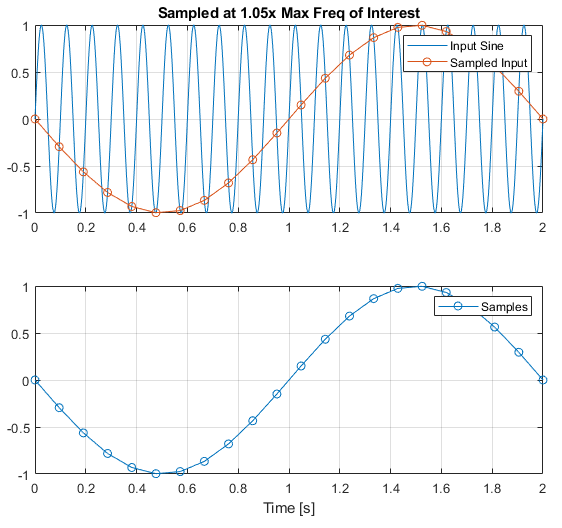
and look at that - a whole new signal is "found"! By sampling at a frequency just above the maximum frequency present in the signal, we've found a 0.5Hz sine wave that doesn't exist - it is just an artifact of our sampling! The same occurs if we sample just below the maximum:
Fn = Fsine * 0.95;
tn = (0:(1/Fn):tFinal);
un = interp1(t,u,tn);
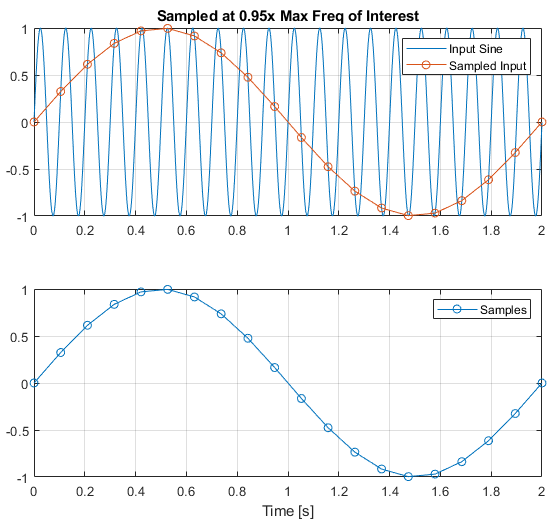
except with a phase shift.
Nyquist-Shannon Sampling Theorem
The reason we are seeing the artifacts above is due to our sampling frequency being too low. The Nyquist-Shannon Sampling Theorem gives a mathematical definition of why this occurs, and the following rule on the sampling frequency required:
⚠ $B < f_s / 2$
where B is the maximum frequency of interest in the signal (i.e. bandwidth we want to measure), and fs is the sampling frequency of our system. Put another way, this states in order to "sufficiently sample" (note, mathematical definition) a signal of B Hz, we would need to sample faster than 2*B Hz. The faster is important, as if you sample at exactly the same frequency as 2*B:
Fn = Fsine * 2;
tn = (0:(1/Fn):tFinal);
un = interp1(t,u,tn);
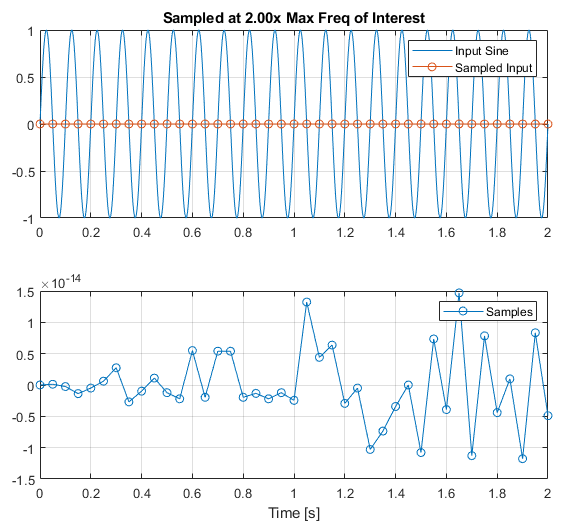
we see we still have aliasing issues! In practice, you will want to sample much faster than 2*B in order to capture a signal of B Hz, shown at even 4*B is not great:
Fn = Fsine * 4;
tn = (0:(1/Fn):tFinal);
un = interp1(t,u,tn);
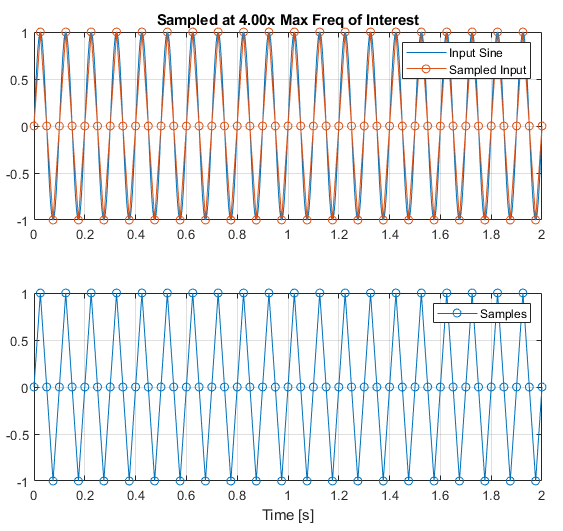
An important definition to remember from this example is the term ⚠ $f_s / 2$, which is known as the Nyquist Frequency. You will see this term come up a lot in filter design and filter analysis, and it is important to know what it means with respect to aliasing and being able to filter signals close to the Nyquist frequency. For example, a low pass filter designed with a sampling frequency of 100Hz cannot have a corner frequency above the Nyquist frequency, therefore limiting the maximum Fc to Fs/2, or ~50Hz.
Anti-Aliasing
There are two ways to approach anti-aliasing, and typically they are combined in order to get the best result.
Anti-Aliasing Analog Low Pass Filter
The most effective, but generally the most expensive, method of implementing an anti-aliasing filter is to add an analog filter to the electronics of your system. This could be a simple RC (1st order) filter, a Sallen-Key opamp-based filter, or a combination such as described here. The main advantage is that the analog filter is "continuous", and therefore there is no sample rate or Nyquist frequency to consider, but it comes at a cost of extra physical components in the design.
To illustrate, consider a system where the signal we are trying to measure is a 1Hz sine wave, but it is corrupted with high frequency noise at 125Hz.
Fs = 1e3; % Assume 1kHz fast enough
Fsine1 = 1;
Fsine2 = 125;
tFinal = 4;
t = 0:(1/Fs):tFinal;
u = sin(Fsine1*2*pi*t) + 0.3*sin(Fsine2*2*pi*t);
If we were to sample this system at 10Hz (i.e. 10x the 1Hz we're interested in, well above Nyquist Frequency), we're going to see the effects of the high frequency noise, aliased into our samples:
Fn = Fsine1 * 10;
tn = (0:(1/Fn):tFinal) + 1e-2; % + Phase offset
un = interp1(t,u,tn);
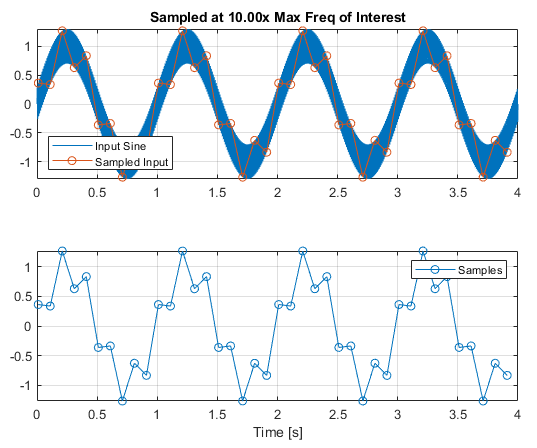
To solve this, we need to low pass filter the input signal to remove this noise and prevent aliasing. "Pretending" we're operating in the analog domain, you could design a Sallen-Key Butterworth 2nd order filter, and filter the signal before it is sampled by the ADC, as below:
N = 2; % order
Fc = 2; % 3dB corner frequency [Hz]
h = fdesign.lowpass('N,F3dB', N, Fc, Fs); % <= Fs here
Hd = design(h, 'butter');
uAA = filter(Hd,u); % Note filter before sample
% Sample at 10x max freq of interest (in this case, 10x1Hz)
Fn = Fsine1 * 10;
tn = (0:(1/Fn):tFinal);
un = interp1(t,uAA,tn);
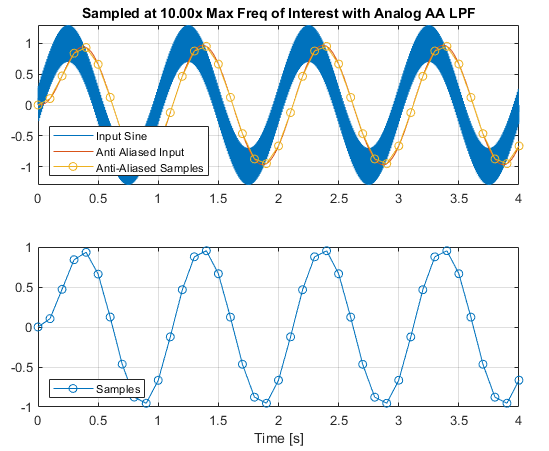
Note the filter has been designed with a very lower corner frequency of 2Hz, thus the phase delay of the filter is quite large. It however effectively attenuates the high frequency noise, allowing the low frequency (10Hz) sampling to avoid any aliasing of the higher frequency corruption.
Anti-Aliasing Digital Low Pass Filter with Oversampling
If you cannot change the hardware of your system, or it's too expensive to add analog filter(s), then you will need to do the work in the digital domain (i.e. software). While this is "free" in the sense it doesn't require more hardware, there will be system changes to get the performance required.
From the definition of Nyquist Frequency above, we know that in order to "sufficiently sample" at 1Hz signal we need to sample at greater than 2x this frequency. For example (only), let's say we sample at 2.5x then maximum frequency of interest, in this case at 2.5Hz. This means we can place the -3dB point of our digital LPF above 1Hz, so we don't attenuate our frequency of interest. This looks like below:
Fn = Fsine1 * 2.5;
tn = (0:(1/Fn):tFinal);
un = interp1(t,u,tn);
% Anti-Aliasing Digital LPF at sample rate
N = 2; % order
Fc = 1.2; % 3dB corner frequency [Hz]
h = fdesign.lowpass('N,F3dB', N, Fc, Fn);
Hd = design(h, 'butter');
% Filter samples
ufilt = filter(Hd,un); % Note filter after sample
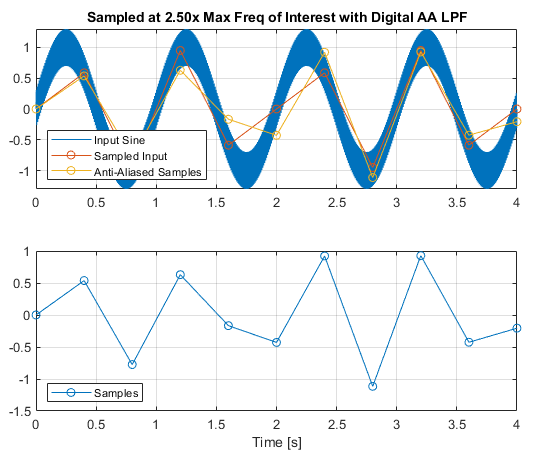
As above, we hardly have a sampled sine wave, nor can really tell if our digital LPF is actually anti-aliasing or not. Therefore it is clear we need to sample much faster to actually have a useful set of samples, with the added benefit of having more flexibility in our filter design. This is known as oversampling, with the design intent to allow better anti-aliasing (rather than improving resolution or reducing noise).
FNyquist = Fsine1 * 2;
FOversample = FNyquist * 4;
tn = (0:(1/FOversample):tFinal) + 1e-2;
un = interp1(t,u,tn);
% Anti-Aliasing Digital LPF
N = 2; % order
Fc = 2; % 3dB corner frequency [Hz]
h = fdesign.lowpass('N,F3dB', N, Fc, FOversample);
Hd = design(h, 'butter');
% Filter samples
ufilt = filter(Hd,un); % Note filter after sample
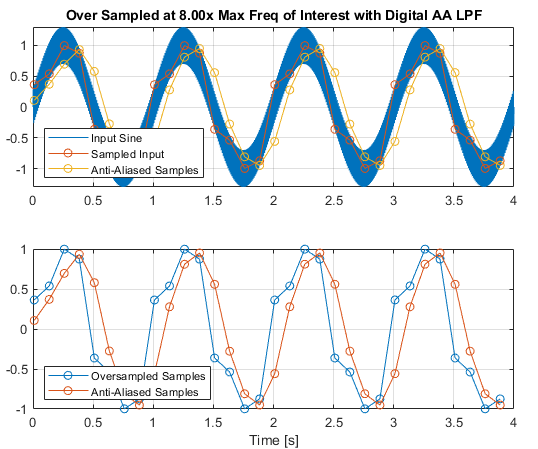
In the example above, an oversampling multiplier of 4 is applied, which is 4x the Nyquist frequency, or 8x the highest frequency of interest. A filter is then designed with a 2Hz -3dB corner frequency, and the higher rate (oversampled) samples filtered to remove the high frequency noise and reduce aliasing. The output looks pretty close to a sine wave, and if a further phase delay could be tolerated, then a higher order digital filter could be used (or different type) to further improve the output.
Note that in order to achieve a higher sample rate for oversampling, the ADC will need to be able to support a higher sample rate, together with the rest of the system (e.g. the digital interface to the ADC may need a higher clock rate, the processor will need to be able to keep up with reading the ADC and there will be a higher computational load due to the filter(s) being called more often).
Anti-Aliasing Combined Analog and Digital Low Pass Filter with Oversampling
In practice most systems will combine an analog front-end anti-aliasing LPF with a digital anti-aliasing LPF in software, together with oversampling.