PID Control: P, PI, PD and PID
The examples below can be found in Control/PID/PID_Examples.m in GNCTools.
Plant Model Example
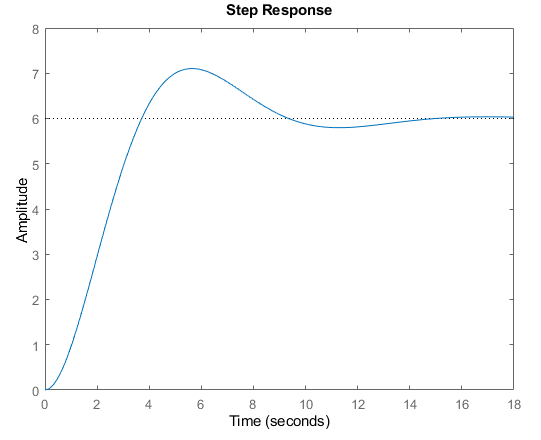
For the examples below, we're going to use the following second order, underdamped, stable, transfer function as our "Plant" model:
step(Gs)
Proportional (P) Control
To begin, let's compare some basic controllers without some of the more advanced functionality. First, proportional only, using the helper methods provided in the example script to create the controller parameter structure (makeControllerParams), make an interesting setpoint and time vector (makeTimeSetpoint) and then simulate using the GNCTools PID controller (simPID):
Ki = 0;
Kd = 0;
pidParams = makeControllerParams(Kp, Ki, Kd, Ts);
[t,r] = makeTimeSetpoint(Ts,tFinal);
simPID(Gs, pidParams, t, r, 0, 'P Only Control');
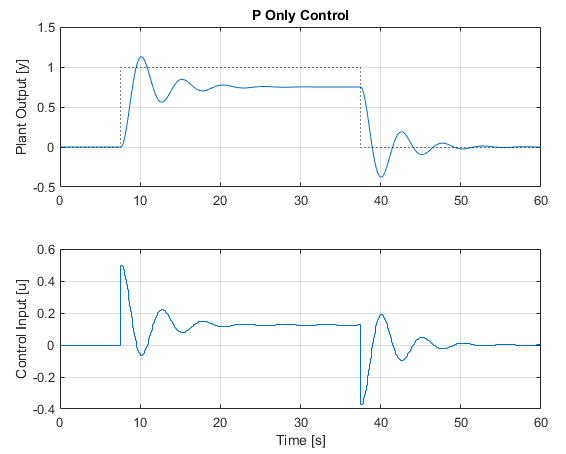
As expected with proportional only control, we see a tracking error (steady-state offset) in the controller, and quite a bit of oscillation. Proportional control is rarely ever used by itself for these reasons.
Proportional-Integral (PI) Control
To address the steady-state offset, we can add some integral action (note the controller form is parallel):
Ki = 0.1;
Kd = 0;
pidParams = makeControllerParams(Kp, Ki, Kd, Ts);
[t,r] = makeTimeSetpoint(Ts,tFinal);
simPID(Gs, pidParams, t, r, 0, 'PI Control');
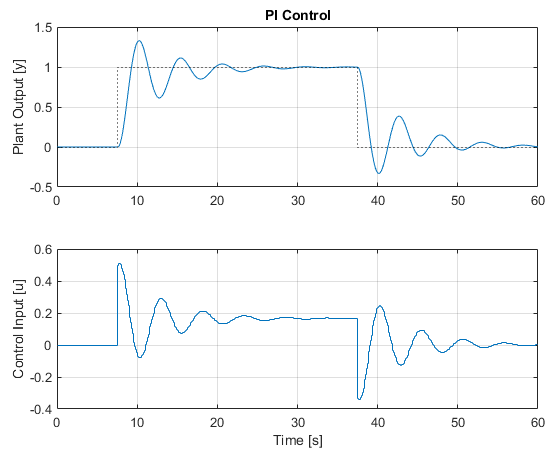
Now we can see the steady-state offset is gone, but the response is still quite oscillatory.
Proportional-Derivative (PD) Control
To address the oscillatory response, we can add derivative action. For this example, we're going to remove the integral action and create a PD controller just to see the effect of adding derivative action, however we will see how steady-state error return:
Ki = 0;
Kd = 0.2;
pidParams = makeControllerParams(Kp, Ki, Kd, Ts);
[t,r] = makeTimeSetpoint(Ts,tFinal);
simPID(Gs, pidParams, t, r, 0, 'PD Control');
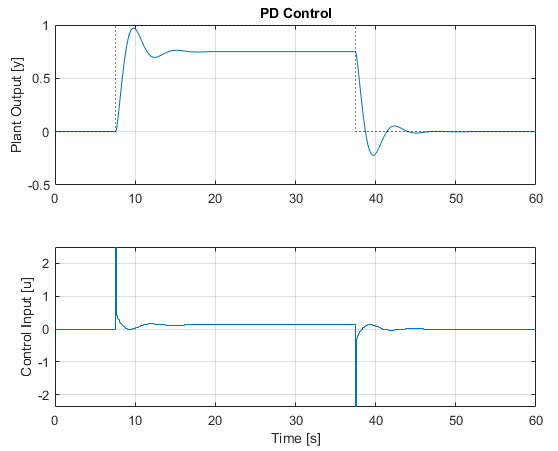
As expected, we see a reduction in the oscillatory behaviour of the system due to the addition of the derivative gain, but our steady-state error is back. Let's wrap it all together as a PID controller in the next section!
Proportional-Integral-Derivative (PID) Control
Taking the benefits of integral action (removing steady-state offset) and derivative action (reducing oscillations) we combine into a PID controller:
Ki = 0.2;
Kd = 0.2;
pidParams = makeControllerParams(Kp, Ki, Kd, Ts);
[t,r] = makeTimeSetpoint(Ts,tFinal);
simPID(Gs, pidParams, t, r, 0, 'PID Control');
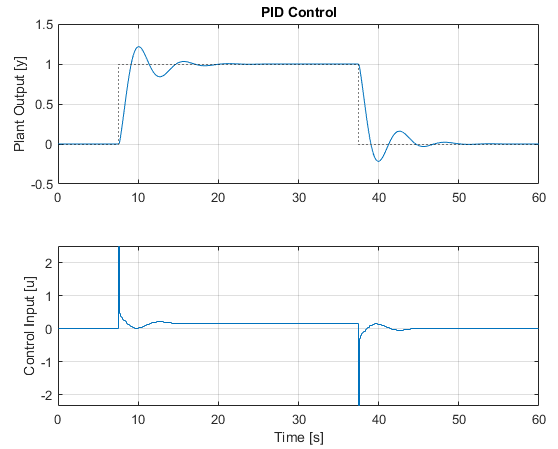
We now have quite reasonable control of the system, albeit with quite 'active' control inputs (noting the large spikes when the setpoint changes). We'll address these with Setpoint Weighting.
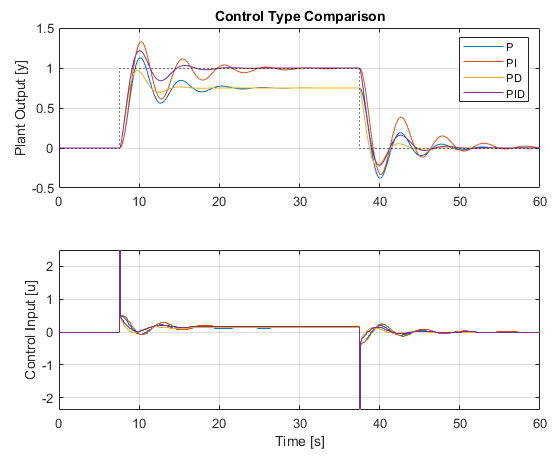
For reference, here is a comparison of the various control schemes above with comparative tuning. Remember that each scheme would normally be independently tuned.