PID Control: Stability Guide
The examples below can be found in Control/PID/PID_Examples.m in GNCTools.
What is Stability?
Once you have tuned your PID controller, and are satisfied with the time domain response (overshoot, rise time, settling time, etc), the next question you should ask is: "How stable is my controller?" To answer this, we need to define first what is a stability.
In classical linear control theory, stability is defined by the location of the poles of your system transfer function. The easiest way to visualize these, is to use pzmap in MATLAB. For continuous systems, the poles (crosses in pzmap) must be on the left hand side of the imaginary axis, and for discrete systems, within the unit circle. Very roughly, the closer the poles are to right hand side/outside the unit circle, the less "stable" your system will be.
Even with this definition, stability is hard to quantify, let alone visualize, so let's look at four example systems in the continuous domain (for ease, the same approach works in the discrete domain too) at how it is applied:
Stable
Using MATLAB's zpk function is convenient way to build transfer functions by explicitly specifying the location of the zeros (numerator roots), poles (denominator roots) and overall gain. Based on the definition above, we will create a system with one real pole, and two imaginary poles, all on the left hand side of the imaginary axis (i.e. their real component is negative):
pzmap(Gs)
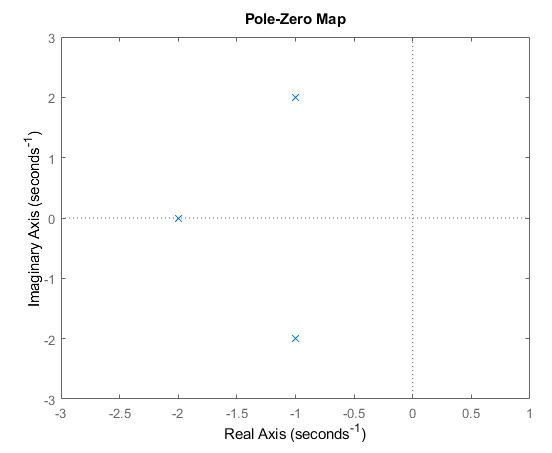
As viewable above, we've created a transfer function with a real pole at -2, and complex conjugate pair at -1+-2i. As the real component of all poles is negative, we expect this system is stable. To see what stable looks like, let's plot the step response and use MATLAB's isstable function:
isstable(Gs)
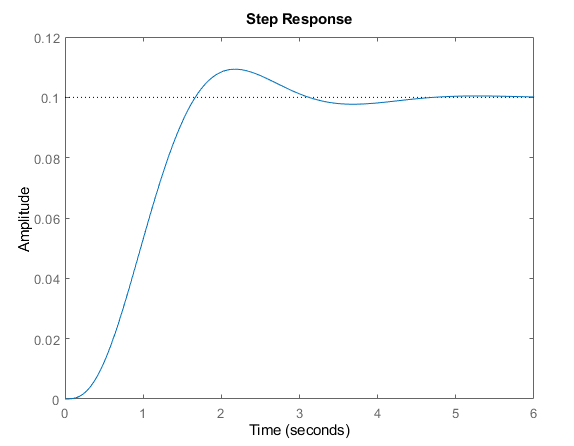
The step response shows a higher order (3rd, in this case) response which is slightly underdamped, but only exhibits a small amount of overshoot and settles to a steady-state quickly. This is what typically expected from a "stable" system. MATLAB also reports this system as stable.
Marginally Stable
Let's repeat and place our complex conjugate pair of poles very close to the imaginary axis:
step(Gs)
isstable(Gs)
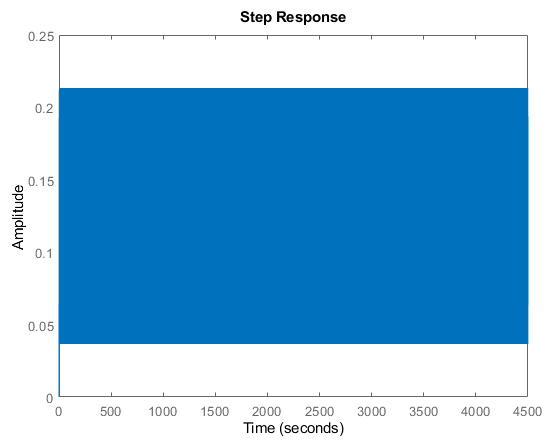
Note the real component of all poles are all still negative, and MATLAB reports the system as stable, but look at the step response:
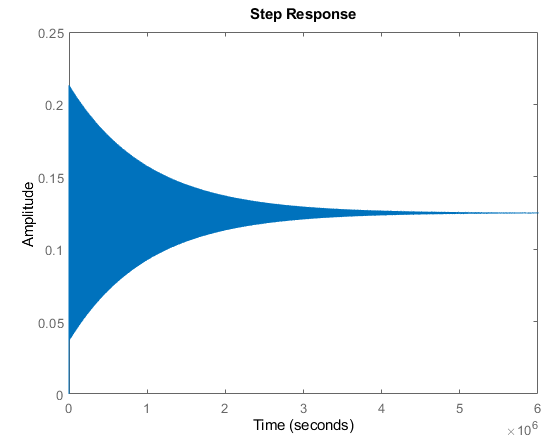
It takes more than 6 million seconds (i.e. more than ~10 weeks) to reach a "steady state"! A control engineer may squirm to agree this system is "technically" stable, but no one would want to work with it! We use the term marginally stable for systems that oscillate for a long time, but the amplitude of the oscillations do decay with time.
Marginally Unstable
Now let's place our complex pair exactly on the imaginary axis, and repeat the analysis:
step(Gs)
isstable(Gs)
MATLAB now reports the system as unstable, and our step response exhibits a persistent (but not increasing, this is important) oscillation:
Given the response is not growing, but has reached a "steady-state" oscillation magnitude, this is referred to as marginally unstable.
Unstable
Finally, let's place our complex pair on the right hand side of the imaginary axis:
step(Gs)
isstable(Gs)
MATLAB also reports this system as unstable, and now our the step response no longer reaches a steady state oscillation:
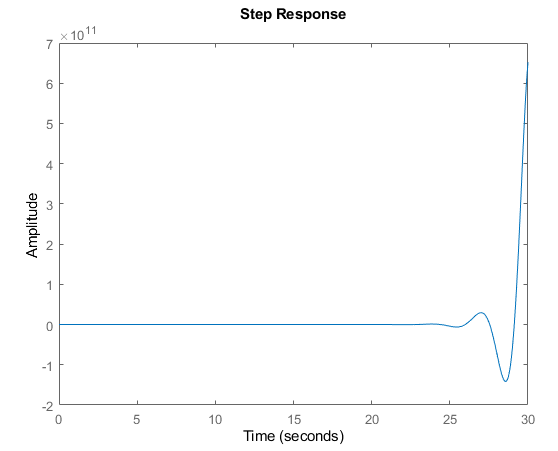
This is what is typically expected as an unstable system.
Summary
It is important to agree on a definition of "instability" or an "unstable system" when working with control systems. Some engineers may look at an decaying oscillatory response and say "unstable", but it really comes to what is standard practice in the industry and application area. Within GNC Tools, provided the amplitude of the oscillations (if any) of a system to a step or impulse decays with time, and the system reaches a steady state constant value, for a non-zero constant input, it is defined as stable, even if it takes a long time!
With respect to poles and their location vs stability, this is one technique that can be used to judge stability, but not one I normally use. It was just a convenient way to generate the four different cases of "stable" plants for this example. We will see some more useful methods to judge stability below.
Open Loop vs Closed Loop Stability
So far we've been looking at stability with respect to an arbitrary transfer function. However we didn't specify whether it was an open loop (controller feedback removed, or simply the plant model without a controller) or closed loop (with feedback) analysis. In practice, the most important aspect is that the closed loop control system is stable, as this is what is actually implemented. However, interestingly enough, most stability analysis is performed on the open loop (no feedback) controller and plant in series, in order to predict the closed loop stability, and stability margins.
When looking at stability, remember that the open loop does not even need to be stable for the closed loop to be stable, as demonstrated below:
step(Gs)
isstable(Gs)
In the above example, the system to control is a pure integrator (e.g. a tank). This system is open-loop unstable because for any constant non-zero input, the system won't reach a steady-state, even though it doesn't oscillate (it is first order). MATLAB confirms this with isstable, and the step response:
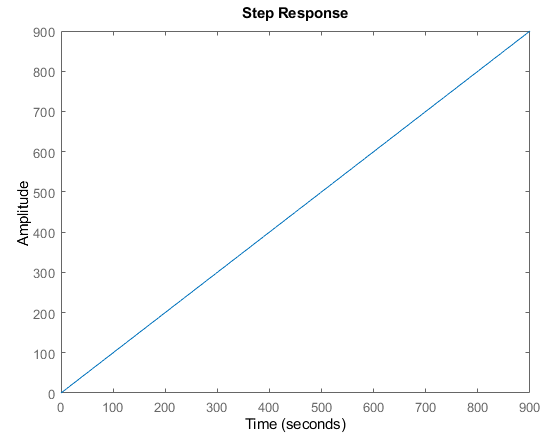
showing it is unstable. We can design a PID controller to control this system using the tuning methods described in tuning guide:
Wc = 1; % Crossover frequency
mlPID = pidtune(Gz,'PIDF2',Wc)
which results in a 2DOF PID controller to stabilize our integrator. To analyze the open-loop Controller + Plant, we can use getComponents to convert our 2DOF PID controller into the "filter" form (and remember, a PID controller is just a transfer function):
[Cfr,Xfr] = getComponents(mlPID,'filter');
% Build Open Loop System with PID Tuned Controller in series
CG_OL = Cfr*Gz;
step(CG_OL)
isstable(CG_OL)
And then reanalyze stability:
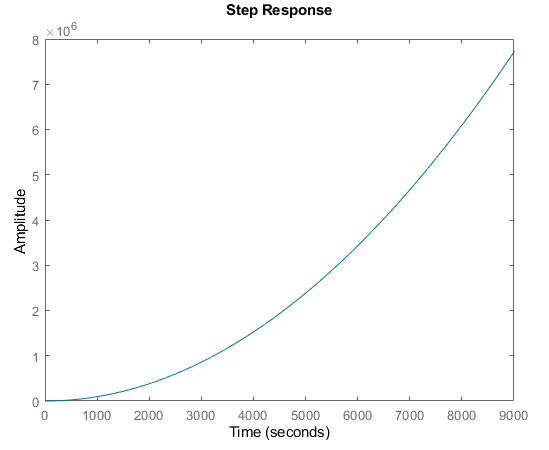
As above, the open loop Controller + Plant is still unstable, confirmed by both the step response and MATLAB. Finally, let's close the loop and reanalyze:
step(CG_CL)
isstable(CG_CL)
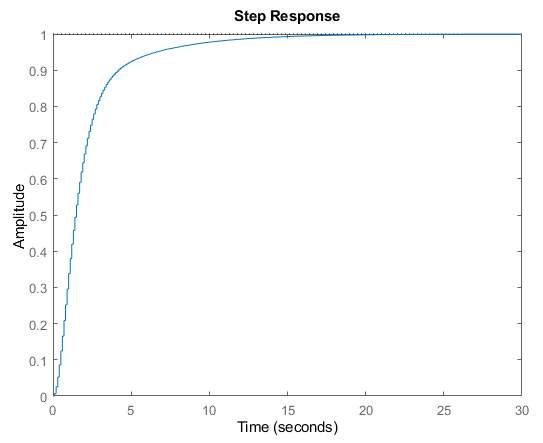
Showing, as expected, we now have a stable control system, even with the initial open loop plant unstable. However it is not immediately clear what we have changed in order to stabilize the closed loop (other than add feedback), nor for what range of gains (or system parameters) will the system remain stable. We can start to improve our understanding of the system and why it is now stable (more than just where the poles are, or using isstable) by moving into the frequency domain, described next.
Frequency Domain Analysis
If your controller and/or system is linear, then there a range of tools to examine and visualize the frequency domain behaviour. In essence, the frequency domain describes your system via gain and phase, as a function of a swept input sine wave of increasing frequency. Let's start with a simple example in the time domain to understand these parameters.
We'll begin with an underdamped second order transfer function. It could be a mass-spring-damper system (such as in a car suspension, or sloshing of liquid in a tank), or other mechanical or electrical system, but regardless of what it represents, it has a specific input frequency which the system will resonate at, and the gain (and frequency) of this resonance could be problematic for a control system.
wn = 1*2*pi; % 1Hz resonance
zeta = 0.025; % Very underdamped
Gs = tf(K*wn^2, [1 2*zeta*wn wn^2]);
While there are analytical methods to determine maximum gain and phase, it is useful to calculate them manually to understand the parameters themselves. Let's simulate the above plant to 3 sine waves of increasing frequency:
t = 0:0.01:30;
u_05 = sin(2*pi*0.5*t);
u_1 = sin(2*pi*1*t);
u_5 = sin(2*pi*5*t);
% Simulate Each & Plot
y_05 = lsim(Gs,u_05,t);
y_1 = lsim(Gs,u_1,t);
y_5 = lsim(Gs,u_5,t);
Plotting input and output on the same axis results in:
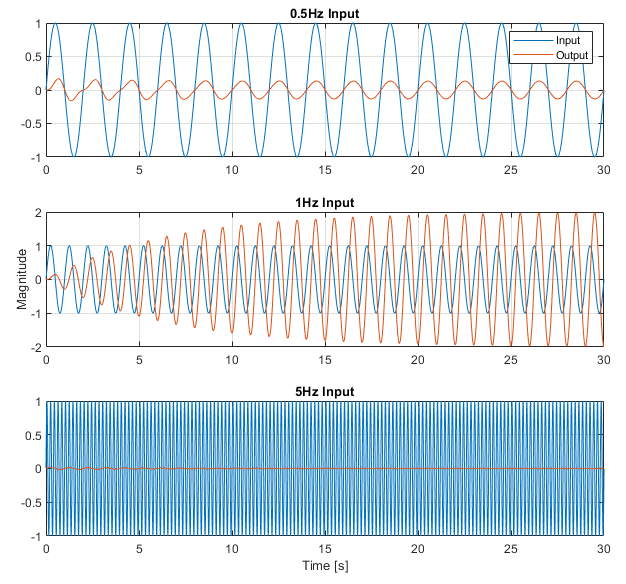
From the above plot we can make the following observations:
- At 1Hz the output is larger than the input (the gain is > 1 or > 0dB), i.e. the system is amplifying the input.
- The gain of the system is much lower at 5Hz, than it is at 0.5Hz, but both attenuate the input.
- There is a phase shift (phase lead or lag, in this case, lag) between input and output in all plots, viewable as a shift in the peaks (or zero crossings) between input and output.
- The system takes some time to reach a steady state gain and phase.
Zooming in on the 1Hz figure, which is the easiest to read, we can compute the gain and phase delay at this frequency:
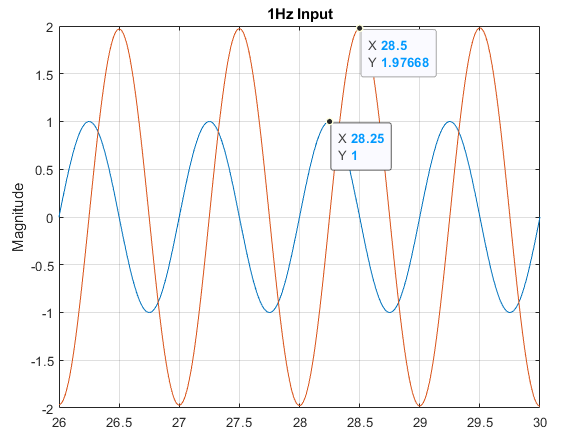
gain_dB = 20*log10(gain)
gain =
1.9767
gain_dB =
5.9187
dt = 28.25-28.5
phase_deg = dt * (360 / 1)
dt =
-0.2500
phase_deg =
-90
So, we can say, if we had a 1Hz sine wave supplied to our system (e.g. an external disturbance, perhaps ruts in a road or vibration in the structure), then this component will amplify the input signal by roughly 2x, with a phase delay of -90 degrees. If this resonance was not appropriately filtered, or the control system designed to be have a lower crossover frequency, then the closed loop system could easily become unstable. This is where the power of frequency domain analysis comes in, especially when looking at the bandwidth of the controller (range of frequencies we want to control over), and any potential instabilities within that frequency range.
Bode Diagrams
So far we've seen we can apply a pure tone (single frequency) sine wave to a transfer function and use the time domain response to estimate the gain and phase. However we can shortcut that process by substituting
⚠ $s = j \omega$
and evaluating the transfer function algebraically:
num = Gs.numerator{:};
den = Gs.denominator{:};
% Substitute s = jw, evaluate tf algebraically
w = 1*2*pi; % Eval at 1Hz
s = j*w;
y = polyval(num,s) / polyval(den,s)
gain_dB = 20*log10(abs(y))
phase_deg = rad2deg(angle(y))
y =
0.0000 - 2.0000i
gain_dB =
6.0206
phase_deg =
-90
Rather than write our own function to do this, we can use MATLAB's bode or bodeplot:
setoptions(h,'FreqUnits','Hz'); grid on;
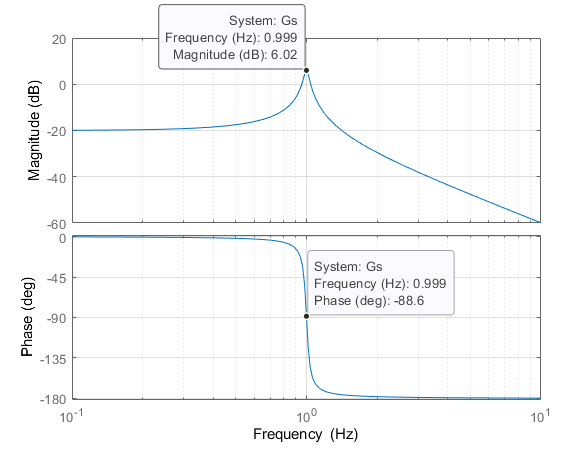
The plot above shows us the gain (top plot) in dB of our transfer function as a function of input frequency, noting the resonant "peak" at 1Hz (as we designed it). The bottom plot shows the phase shift (negative = lag/delay, positive = lead) as a function of input frequency.
The bode plot is one of the most useful tools the control engineer has in their toolkit, and is the "cornerstone" of frequency domain analysis.
Nichols Chart
Another way to view the information in a bode diagram is a Nichols chart, which plots the gain vs phase on an X-Y plot:
setoptions(h,'FreqUnits','Hz'); grid on;
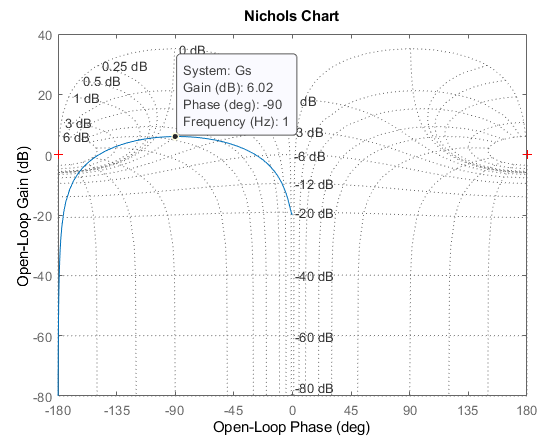
While less commonly used, the Nichols chart is incredibly useful for understanding the dynamics of a system, together with stability margins. In the plot above, the red crosses dictate where the gain of the system is 1 (0dB), and the phase shift is a 360 degree multiple of a 180 degree phase shift (e.g. -180, -540 deg, or 180, 540 deg, etc), together with the system response in blue. The closer the blue line is to the red crosses, the less "stability margin" is present in the system, as we will see below. This makes the Nichols chart convenient to quickly judge stability when compared to e.g. a bode plot.
Gain and Phase Margin
One definition of stability that we have not explored so far is when the following occurs:
⚠ $1 + G(j \omega) = 0$
which states if the gain of the open loop system is 1 (⚠ $|G(j \omega)| = 1$) and the phase shift of the open loop system is -180 degrees (or +180, -540, etc, via ⚠ $\angle G(j \omega) = -180^\circ$), then by definition the system is unstable. Basically what happens is with a 180 degree phase shift and unity (or higher) gain, then once feedback is applied and the loop closed (e.g. via a controller), then the system is guaranteed to oscillate due to positive feedback (i.e. becomes marginally unstable -> unstable). This relationship allows us to define stability margins with respect to this condition, known as Gain and Phase Margin, both computed with respect to the open loop system:
- Gain Margin
- The difference in gain between 0dB and the system gain, computed where the phase shift is -180 degrees (modulo 360). This is effectively the amount of gain that can be added to the open loop system before it becomes unstable. Gain margin must be positive for stability.
- Phase Margin
- The difference in phase between the system phase and 180 degrees, computed where the gain is 1 (0 dB). This is effectively the amount of phase delay the controller and/or filtering (or system dead time) can add to the open loop system before it becomes unstable. Phase margin must be positive for stability.
From the above definitions and practical experience, the following stability margins are generally accepted for "best practice":
- Gain Margin:
⚠ $G_M >= 3 \text{dB}$, preferably⚠ $>= 6 \text{dB}$ - Phase Margin:
⚠ $P_M >= 30^\circ$, preferably⚠ $>= 60^\circ$
MATLAB allows us to compute stability margins using margin, as well view them on any frequency domain plot. This is done for the combined controller + plant in open loop. To demonstrate, we'll design a PID controller for the (very) oscillatory system above that we've been analyzing:
Gz = c2d(Gs, Ts);
% Design Controller
Wc = 0.025*2*pi; % Crossover frequency
mlPID = pidtune(Gz,'PIDF2',Wc)
Note the extremely low crossover frequency specified - 0.025Hz, versus the resonant frequency of the system we're controlling at 1Hz. This is required to stabilize this system in the absence of any filtering. Basically we're designing a very slow controller to avoid exciting the 1Hz resonance via any control inputs. So much so, that the resulting controller returned by pidtune contains no derivative action - it is purely a PI controller!
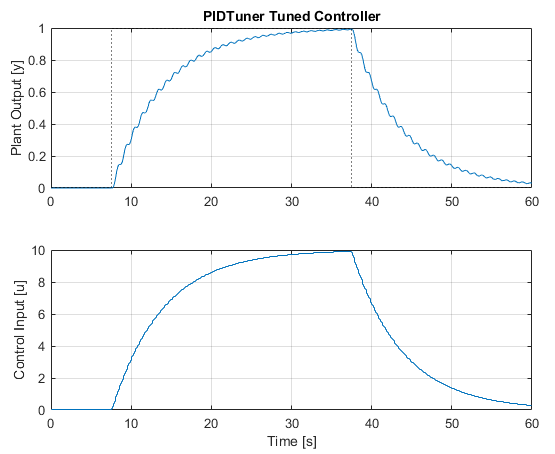
As expected, the control response is very slow. We then use the same technique as above to convert the PI(D) controller to filter form to analyze the open loop controller + plant response, and compute the stability margins:
% Build Open Loop System
CG_OL = Cfr * Gz
% Compute & display stability margin
margin(CG_OL);
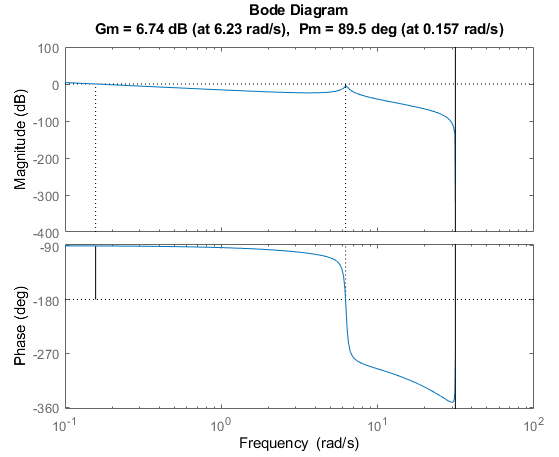
From the above plot and analysis, we have designed a controller that has both sufficient gain margin (6.74dB) and phase margin (89.5deg) to cover expected modelling errors and system performance issues (e.g. delays in sampling, processing time), as well as plenty of phase margin to spare to investigate filtering the resonance, rather than suffering a poor rise time of the controller. This is an important observation in itself however - we have tuned a control system that meets our stability margin goals, but at a sacrifice of the time domain performance. There is typically always a compromise between these two sides; stability vs performance, and accepting lower stability margins is often required to meet setpoint tracking and/or disturbance rejection targets.
Effect of Reducing Gain Margin
For interest, we can increase the gain of our controller and see what would happen to our closed loop performance:
CG_CL_nom = Xfr*feedback(Gz*Cfr,1);
% Build Closed Loop System with 0db Gain Margin
[Gm,Pm] = margin(CG_OL);
CG_CL_0db = Xfr*feedback(Gz*Gm*Cfr,1);
% Plot tuned and increased gain system
stepplot(CG_CL_0db, CG_CL_nom)
xlim([0 tFinal])
grid on;
legend('0db GM','PID Tuned Original')
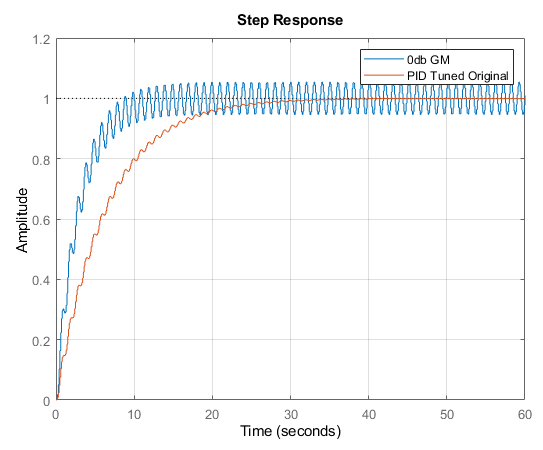
As viewable above, with no gain margin, this system will oscillate forever and thus be deemed (marginally) unstable.
Effect of Reducing Phase Margin
Additionally for interest, we can arbitrarily add dead time to the system to represent additional phase delay and see what would happen to our closed loop performance:
theta = 6; % 6 seconds dead time - heaps!!
Gs_delay = exp(-theta*s);
Gz_delay = c2d(Gs_delay, Ts);
% Build Closed Loop System with reduced phase margin
CG_CL_reducedPM = Xfr*feedback(Gz*Gz_delay*Cfr,1);
% Plot tuned and increased gain system
stepplot(CG_CL_reducedPM, CG_CL_nom)
xlim([0 tFinal])
grid on;
legend('Reduced PM','PID Tuned Original')
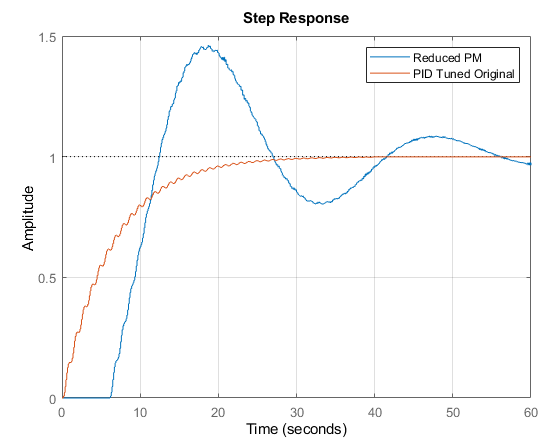
Generally for a system with a sampling interval of 0.1s, if 6s of dead time was unmodelled, you would expect the controller to massively fail! However due to the large amount of phase margin in this system (89.5deg), even 6s of unmodelled deadtime results in a "comfortable" 35deg of phase margin, which while still (very) oscillatory, as above, is not close to being unstable.
Summary
In both cases above we've shown that reducing the stability margins increases oscillation, which is generally a good indicator of being on a stability limit, or having low stability margin somewhere. This is why you will see many control loops in practice tuned to have a critically damped response (especially in the process control world), rather than exhibit any overshoot/oscillation, as it "instinctively" feels more stable. However you now have the tools to tune PID controllers and analyze closed loop stability as you like, and trade time domain performance against stability margins with ease.
Parameter Uncertainty
One final topic worth discussing is parameter uncertainty, or, put another way, how well have you modelled your system? Did you do all your stability analysis using a FOPDT model which only "sort of" captures the dynamics of your system? Is your system actually nonlinear and the gain changes depending on the sign on the input (e.g. a hot water cylinder with active heating and passive cooling), or the gain or damping changes as a function of some other internal parameter? Once you are getting into this level of analysis the "correct" way to design controllers and ensure stability is using Robust Control, which MATLAB has a nice toolbox to support. However be aware it is very mathematics-heavy, and generally a "guaranteed stable" controller will compromise (heavily) on time domain performance, as we have seen above.
An alternative approach is to tune your control system for your "nominal" parameters, with appropriate stability margins, then simulate/analyze your control system across a range of scattered parameters (with ranges based on e.g. test data, analysis) and ensure it remains stable. This is known as a Monte Carlo Simulation. If your parameter space is small enough (i.e. ~10-15 parameters), a Latin Hypercube Sampling (LHS) approach can be used to generate parameter combinations, to ensure all extremums are tested, otherwise an appropriately chosen random distribution can be used instead. The example below uses LHS across defined parameter ranges of our plant model, in addition to some uniformly chosen random parameter sets:
K = [0.08 0.12]; % Low gain
wn = [0.7 1.3]*2*pi; % ~1Hz resonance
zeta = [0.02 0.03]; % Very underdamped
% Design & Simulate Nominal Controller
K_nom = mean(K);
wn_nom = mean(wn);
zeta_nom = mean(zeta);
Gs_nom = tf(K_nom*wn_nom^2, [1 2*zeta_nom*wn_nom wn_nom^2]);
Gz_nom = c2d(Gs_nom, Ts);
Wc = 0.025*2*pi; % Crossover frequency
mlPID = pidtune(Gz_nom,'PIDF2',Wc);
pidParams = makeControllerParams(mlPID.Kp, mlPID.Ki, mlPID.Kd, mlPID.Ts, mlPID.Tf, -Inf, Inf, mlPID.b, mlPID.c);
[t,r] = makeTimeSetpoint(Ts,tFinal);
[u_nom,y_nom] = simPID(Gs_nom, pidParams, t, r);
% Monte Carlo Sim with LHS paramset
params = lhs({K,wn,zeta},100);
h = zeros(length(params),1);
Gs_mc = tf(zeros(1,1,length(params)));
for i = 1:length(params)
% Sim controller with scattered plant model
K = params{i}(1);
wn = params{i}(2);
zeta = params{i}(3);
Gs_mc(:,:,i) = tf(K*wn^2, [1 2*zeta*wn wn^2]);
[u,y] = simPID(Gs_mc(:,:,i), pidParams, t, r);
% Add to plot
subplot(211)
h(i) = plot(t,y,'color',[0 0.447 0.741]);
hold on;
subplot(212)
stairs(t,u,'color',[0 0.447 0.741]);
hold on;
end
% Complete Plot
subplot(211)
h(end+1) = plot(t,y_nom,'color',[0.9290 0.6940 0.1250]);
stairs(t,r,'k:');
hold off; grid on;
ylabel('Plant Output [y]');
title('Monte Carlo Simulation of PI Control of Oscillatory System');
legend([h(1),h(end)],{'Scattered','Nominal'},'location','best')
subplot(212);
stairs(t,u_nom,'color',[0.9290 0.6940 0.1250]);
hold off; grid on;
ylabel('Control Input [u]');
xlabel('Time [s]');
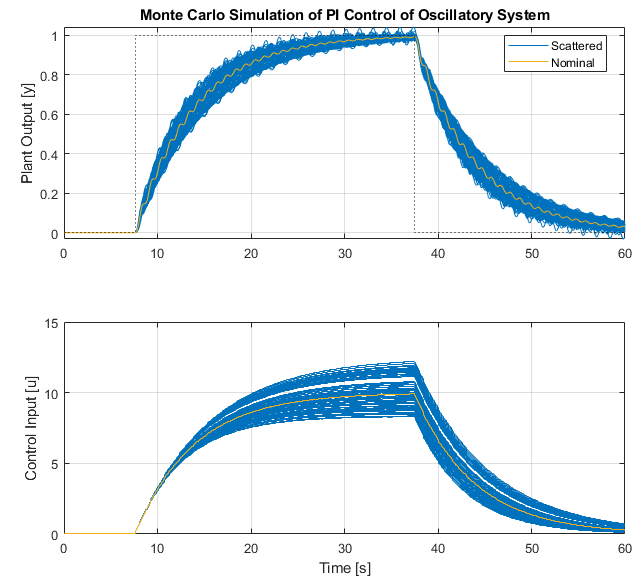
Observing the output time domain Monte Carlo responses shows nothing obvious (Hint: Simulate for longer to see issues...), with a few oscillations that could be expected given the range of parameters we simulated across. However given we are now experts in Frequency Domain analysis, we can plot all open loop controller and plant responses on a Nichols chart to visually check for stability margin concerns:
Gz_mc = c2d(Gs_mc,Ts);
CG_OL = Cfr * Gz_mc;
h = nicholsplot(CG_OL);
setoptions(h,'FreqUnits','Hz'); grid on;
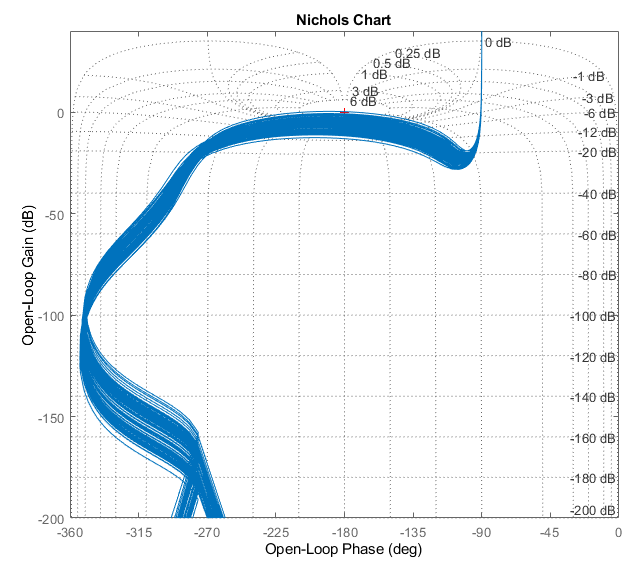
Where we can immediately spot one (or more) systems very close to a red cross, remembering this is a point of guaranteed instability! Zooming in we can find which system(s) are on the edge of stability:
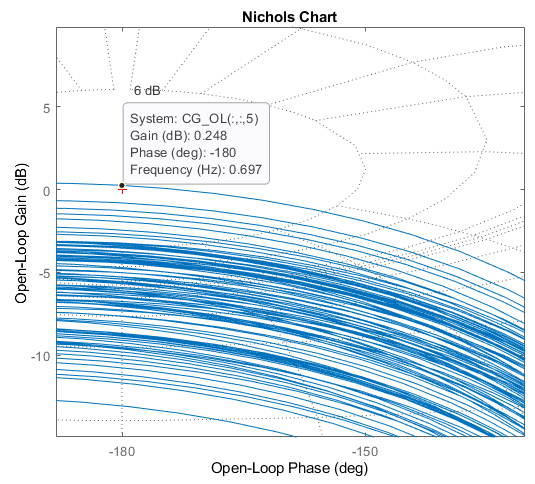
while there are a lot of systems with very low gain margin, one has negative gain margin (i.e. > 0dB gain at 180deg phase shift), which is shown as index 5. We can then examine the actual margin of this system, together with the scattered parameters that created this system:
params{5}
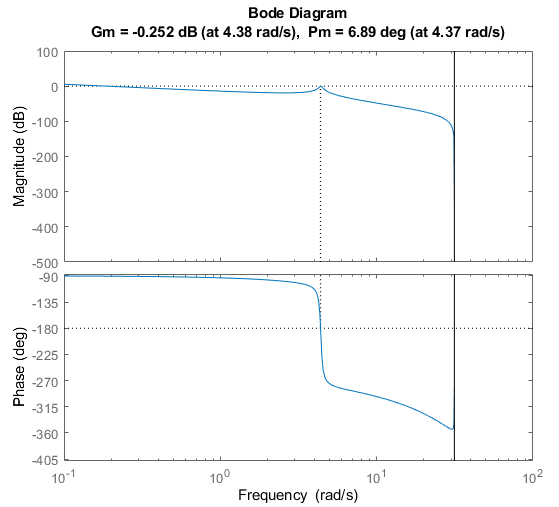
At this point we could go back and take a hard look at the parameter ranges, and see whether we really "think" this parameter combination is physically possible. This could be additional tests to lower uncertainty, or further analysis. Or, if we trust the parameter ranges, "detuning" (i.e. reducing the bandwidth) of the controller is required in order to have positive stability margins across all scattered plant models. Alternatively, you could add a digital filter, as shown below.
Improving Performance via Filtering
While not strictly part of the stability guide, this is a little extra for experts. For the case we've been analyzing so far we've had to compromise on poor control performance (very slow) by designing our controller bandwidth to be much lower in frequency than the resonance at 1Hz. One way to avoid this is to filter the input to the plant, so frequencies around the resonant peak are attenuated and it doesn't get "excited", and thus the controller bandwidth can be increased, and overall loop performance increased. We can do this when we have sufficient phase margin to play with, which we do in this case.
The filter design section will cover filter design, but very briefly we will design a 4th order Butterworth Notch Filter with the -3db corner frequencies chosen either side of our 1Hz resonance:
N = 4; % Order
Fc1 = 0.8; % First Cutoff Frequency
Fc2 = 1.25; % Second Cutoff Frequency
h = fdesign.bandstop('N,F3dB1,F3dB2', N, Fc1, Fc2, 1/Ts);
Hd = design(h, 'butter');
[num,den] = tf(Hd);
GzFilt = tf(num,den,Ts);
% Bode Comparison For Interest
h = bodeplot(Gz,GzFilt,GzFilt * Gz);
setoptions(h,'FreqUnits','Hz','PhaseWrapping','off'); grid on;
legend('Plant','Filter','Plant + Filter')
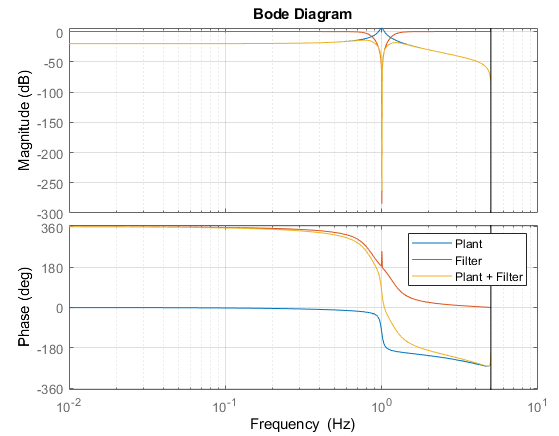
As shown in the above bode plot, our filter (in red) is designed as a band-stop notch filter to attenuate frequencies around 1Hz. When placed in series with the plant transfer function, the resulting gain plot (in yellow) shows the resonant peak is basically removed, with minimal additional low frequency phase shift (which is what we want, generally).
We can now design a new PI(D) controller for this system with increased bandwidth (4x in fact) and compare the controlled response without the filter:
mlPID = pidtune(GzFilt * Gz,'PIDF2',Wc)
uMin = -Inf;
uMax = +Inf;
rRampMax = +Inf;
pidParams = makeControllerParams(mlPID.Kp, mlPID.Ki, mlPID.Kd, mlPID.Ts, mlPID.Tf, uMin, uMax, mlPID.b, mlPID.c, rRampMax);
[t,r] = makeTimeSetpoint(Ts,tFinal);
[u_notch,y_notch] = simPID(GzFilt * Gz, pidParams, t, r);
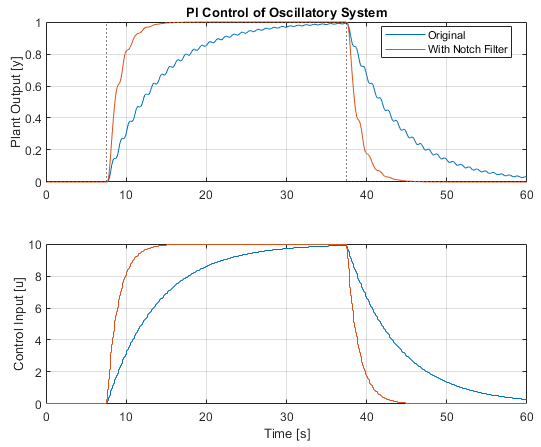
Showing we've substantially improved the time domain performance of the control system by adding the filter! And to ensure the stability margins haven't been compromised, let's use a Nichols chart (right click the chart, Click Characteristics, All Stability Margins):
% Build Open Loop System
CG_OL = Cfr * GzFilt * Gz
% Compute stability margin
[Gm,Pm] = margin(CG_OL)
h = nicholsplot(CG_OL);
setoptions(h,'FreqUnits','Hz'); grid on;
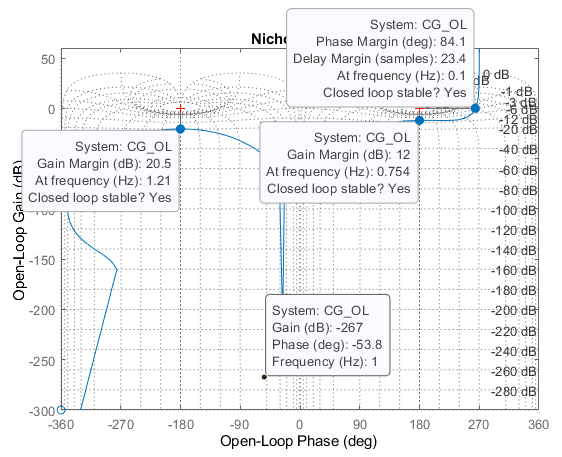
As shown we've slightly reduced the phase margin to 84.1 degrees by adding the filter (generally expected), but actually improved the gain margin to 12dB! Filtering is an extremely powerful way to improve control performance at the cost of phase margin (and some other numerical and CPU performance considerations). Just ensure you don't go "overboard" with filtering attenuation or bandwidth, as you will adversely effect the phase margin and overall loop stability.