PID Control: Tuning Guide
The examples below can be found in Control/PID/PID_Examples.m in GNCTools.
Manual Tuning
Most of us at one time or another have attempted to tune a PID controller 'by hand' (i.e. manually). We might be in a rush, or simply haven't spent the time to develop a model of the system we're trying to control and thus can't use automated methods. If you are faced with this situation, then this table is a good reference, reproduced below which describes the effect of increasing each gain independently:
| Parameter | Rise Time | Overshoot | Settling Time | Steady State Error | Stability |
| Kp | Decrease | Increase | Small Change | Decrease | Degrade |
| Ki | Decrease | Increase | Increase | Eliminate | Degrade |
| Kd | Minor Change | Decrease | Decrease | No effect | Improve for small Kd |
Remember the table above is for changing any parameter independently, and is only a generalization. It should be used as a guide only, and a more rigorous modelling and analysis approach used instead where time allows.
First Order Modelling
As a control engineer, investing in a model is always a worthwhile exercise as it provides insight into the operation of the system, together with the ability to perform stability analysis and automated tuning. However deriving a detailed, physics-based model (i.e. white or grey box) can be very time intensive and require specialized knowledge outside your technical domain. Therefore if your plant/process is open loop stable (i.e. a judicially chosen constant input won't damage the system or make it unstable), then a common first order approximation is a First Order Plus Dead Time (FOPDT) model, which is a simple black box/empirical model:
⚠ $G(s) = \frac{K e^{-\theta s}}{\tau s + 1}$
where K is the process gain, ⚠ $\tau$ is the process (first order) time constant, and ⚠ $\theta$ is the process time delay (dead time).
The nice thing about this model is that it captures most dynamics of reasonably damped systems (e.g. ⚠ $\zeta > 0.8$) that are required to obtain good enough control with a PID controller. To illustrate, we're going to use a new second order plant model to generate some "real data" that captures a step test of the system. We will then use this data to fit a FOPDT model, and then use the fitted model for tuning our controller. To begin, the "true" plant we will be modelling and controlling:
Gs_true = tf(1.2, [0.5 0.5 0.2]);
step(Gs_true)
% Constants
Ts = 0.1;
tFinal = 60;
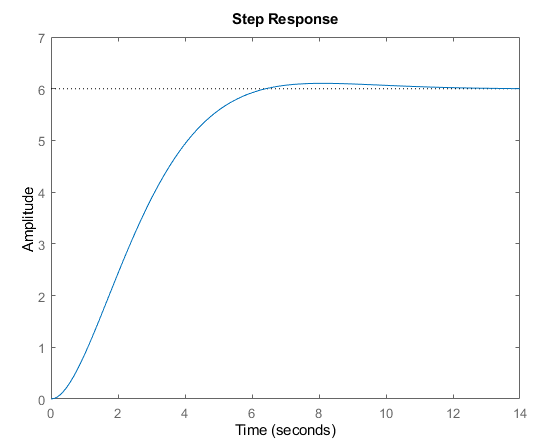
As above, the response is obviously second order (or higher) from the "S-shape" of the curve, together with the overshoot. We will use this model to generate some interesting measurement data, from some simulated step tests of it:
Gz_true = c2d(Gs_true, Ts);
% Generate some sample "measurement data"
t = 0:Ts:tFinal;
ustep = ones(size(t)); n = length(ustep);
ustep(ceil(n/2):end) = -0.5;
rng('default'); % Same seed each run, just for Wiki examples
ymeas = lsim(Gz_true,ustep,t) + sqrt(0.01) * randn(n,1);
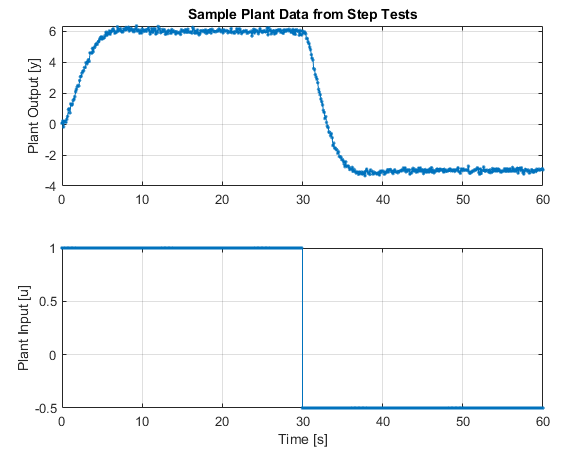
Note the above step tests are pretty basic, and you may find you need more over the operating range of your plant to characterize its behaviour. Always try and do step tests in both directions, and near the typical operating point. Next, we will attempt to fit a FOPDT model to this data. We can estimate graphically the initial parameters guesses for the optimizer, by simply looking at the plot:
- K
- Input of 1 results in a output of 6; gain is ~6
⚠ $\theta$- The system takes approximately 0.5 seconds to begin to move;
⚠ $\theta$is ~0.5 s. ⚠ $\tau$- The system reaches 1 time constant (63.2% of the final value) after approximately 2.75 seconds; removing dead time
⚠ $\tau$is ~2.25.
K0 = 6;
theta0 = 0.5;
tau0 = 2.75 - theta0;
% Note requires OPTI Toolbox: https://www.controlengineering.co.nz/Wikis/OPTI/
Gs_fit = fitFOPDT(t,ustep,ymeas,K0,tau0,theta0,'FOPDT Fit')
The result of the above (simple, naive) example fitting routine is as follows:
6.044
exp(-0.865*s) * -----------
1.847 s + 1
Continuous-time transfer function.
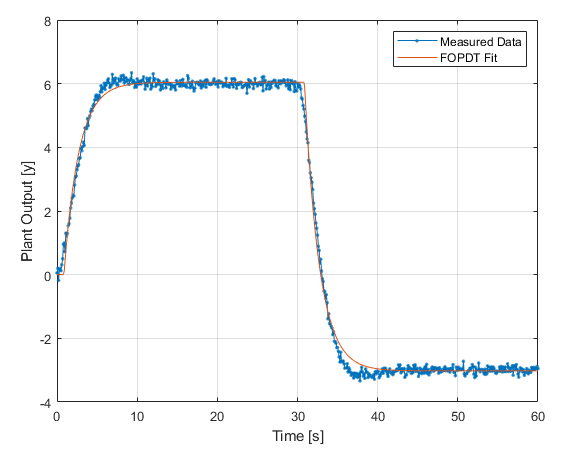
Showing our initial guesses weren't too far off, and the optimizer has found a solution that approximates the plant response quite well. We now have a model of our plant we can use for more powerful tuning methods and analysis!
Automated Tuning
Once you have a model of the plant you are trying to control, you can use the powerful tuning algorithms included with MATLAB's Control Systems Toolbox. While the literature is rich with tuning methods and algorithms, MATLAB has done a pretty good job of getting their tuning routines robust and effective. My favourite is pidtune (and associated GUI, pidTuner), which we will use below.
First, discretize our fitted FOPDT model at the sampling rate we want our controller to run at, then tune a 2DOF PID controller with a crossover frequency of 1 rad/s:
Wc = 1;
mlPID = pidtune(Gz_fit,'PIDF2',Wc)
this results in the following PID controller:
Ts 1
u = Kp (b*r-y) + Ki ------ (r-y) + Kd ----------- (c*r-y)
z-1 Tf+Ts/(z-1)
with Kp = 0.344, Ki = 0.0873, Kd = 0.0786, Tf = 0.145, b = 0.937, c = 0.0148, Ts = 0.1
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.
You can see MATLAB has tuned all parameters for us (including the derivative filter Time Constant and Setpoint Weights), and returned a pid2 object. We can simulate this controller with our fitted FOPDT model to see what response MATLAB has designed for us:
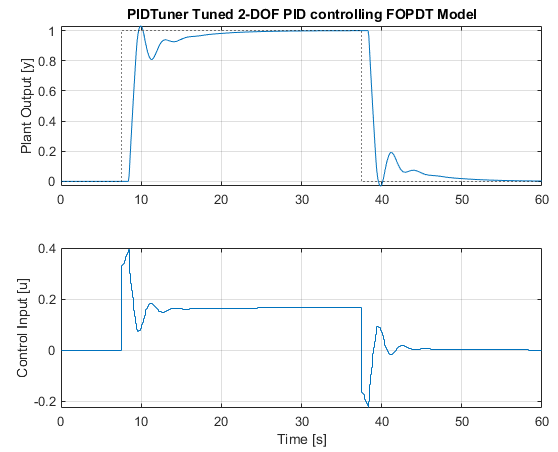
Which is not too bad. We could adjust the crossover frequency to obtain faster or slower responses, or modify the gains manually if we want to fine tune it. With the magic of simulation, we can also check what would happen if we were to use this PID controller with the true plant, and actually implement it:
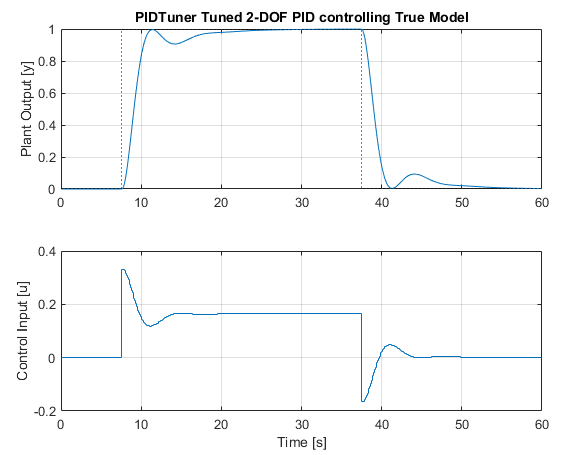
As our FOPDT model was a good approximation of the true system, the controller that MATLAB designed does well controlling the true plant as well. I recommend experimenting with the pidTuner GUI for more control of the MATLAB designed controller as well.
Note more information on the frequency domain is provided in the Stability Guide, but roughly the crossover frequency from MATLAB's help is:
Second Order Modelling
If you have a system that exhibits significant overshoot (i.e. is quite underdamped) then a FOPDT model will typically not capture the dynamics correctly, and the above method won't work. In this case using a higher order model can be used, but noting fitting these is much more difficult. The classic second order system with dead time is:
⚠ $G(s) = K e^{-\theta s} \frac{\omega^2_n}{s^2 + 2 \zeta \omega_n s + \omega^2_n}$
where K is the process gain, ⚠ $\omega_n$ is the undamped natural frequency (frequency the system would oscillate at with no damping), ⚠ $\zeta$ is the damping ratio and ⚠ $\theta$ is the process time delay (dead time).
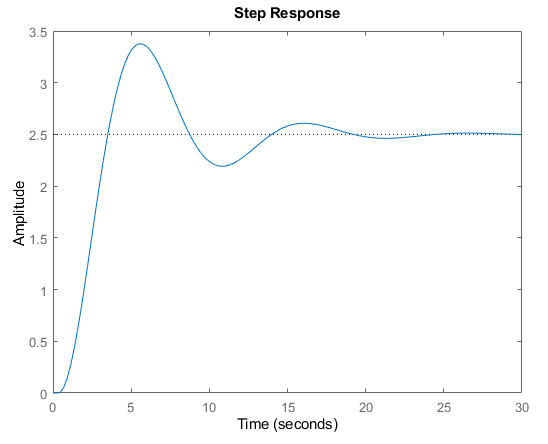
As above, we'll create a sample second order system to generate some interesting data, and try fit it and design a controller for it:
Gs_true = tf(0.5, [0.5 0.2 0.2],'IODelay',0.35);
step(Gs_true)
% Constants
Ts = 0.1;
tFinal = 60;
and generate some measurement data to fit in the same way as for the FOPDT example, resulting in:
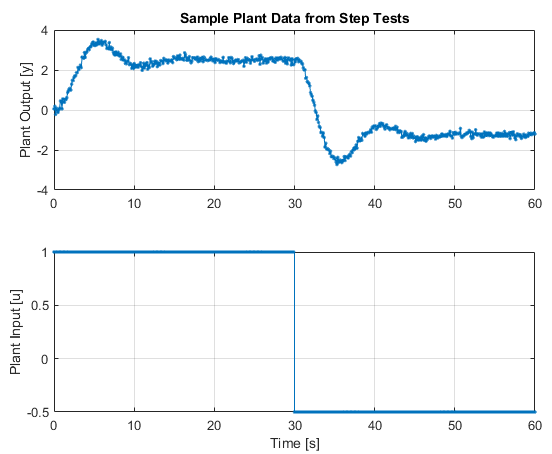
With a SOPDT model, there are now four parameters to fit and each requires an initial guess (which can be done graphically):
- K
- Input of 1 results in a output of 2.5; estimate gain as ~2.5
⚠ $\omega_n$- Time between first two peaks is ~6s; estimate
⚠ $\omega_n$as ~1 rad/s (1/6*2*pi) ⚠ $\zeta$- Looks quite underdamped; estimate
⚠ $\zeta$as ~0.5. ⚠ $\theta$- The system takes approximately 0.3s to begin to move; estimate
⚠ $\theta$as ~0.3 s.
K0 = 2.5;
wn0 = 1;
zeta0 = 0.5;
theta0 = 0.3;
% Note requires OPTI Toolbox: https://www.controlengineering.co.nz/Wikis/OPTI/
[Gs_fit,K,wn,zeta,theta] = fitSOPDT(t,ustep,ymeas,K0,wn0,zeta0,theta0,'SOPDT Fit')
The result of the above (simple, naive) example fitting routine is as follows:
0.9823
exp(-0.311*s) * -----------------------
s^2 + 0.3972 s + 0.3938
Continuous-time transfer function.
K =
2.4945
wn =
0.6275
zeta =
0.3165
theta =
0.3109
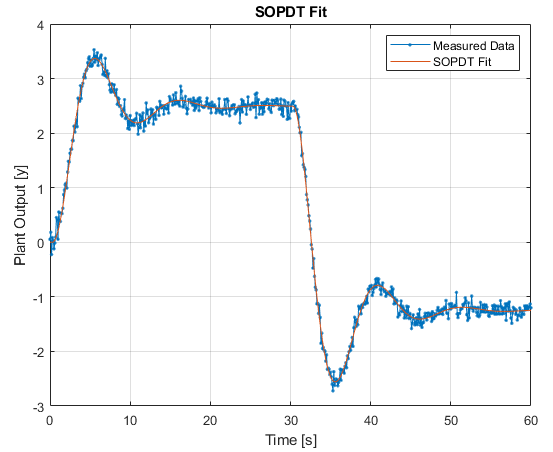
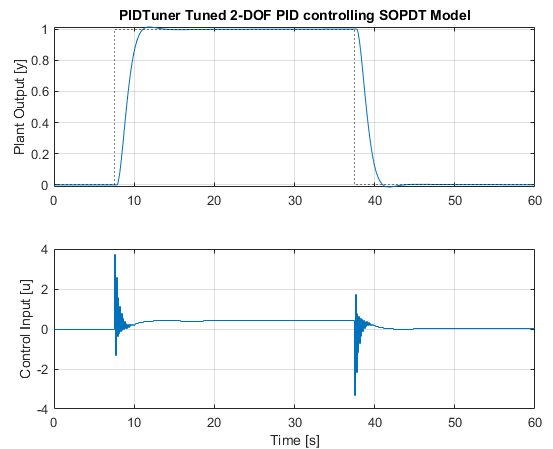
Given we a fitting a model with the same model structure and number of parameters, together with a good starting guess, we should expect a pretty good result, which is shown above. The deviation between estimated and true parameters lies predominately in the measurement noise, which could be filtered if desired. We can then use the same pidtune routine to tune a 2DOF PID controller, and simulate the closed loop response:
Wc = 1.3; % Crossover frequency
mlPID = pidtune(Gz_fit,'PIDF2',Wc)
this results in the following PID controller:
Ts 1
u = Kp (b*r-y) + Ki ------ (r-y) + Kd ----------- (c*r-y)
z-1 Tf+Ts/(z-1)
with Kp = 0.589, Ki = 0.0804, Kd = 1.04, Tf = 0.0567, b = 1.46, c = 0.157, Ts = 0.1
Sample time: 0.1 seconds
Discrete-time 2-DOF PIDF controller in parallel form.
Occam's Razor
You may be tempted to keep increasing the model order, or adding more parameters to your models in order to "better" fit your measurement data, however a well-known principle in many fields is that of Occam's Razor. Summarizing, it basically means to always prefer the simplest solution, or in our case, the model with the least number of parameters that is "good enough" for the purposes of the model. As an example, if your plant data shows an overdamped (or critically damped) response - why try to fit a second order model to it? You may find a FOPDT fit is perfectly adequate for the purposes of controller tuning, and reduces the number of parameters to guess and fit.
Be judicial in choosing model order, and modelling in general. A spline or high order polynomial might "look better", but you may also find a quadratic performs just as well.