System of Constrained Nonlinear Equations (SCNLE)
Problem Definition
A SCNLE has the following form:
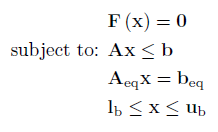
Where F is a vector function containing the nonlinear equations.
Linear Inequalities
A is a m x n dense matrix, b is a m x 1 vector.
Linear Equalities
Aeq is a k x n dense matrix, beq is a k x 1 vector.
Decision Variable Bounds
lb and ub are n x 1 vectors, where -inf or inf indicate an unbounded lower or upper bound, respectively.
The goal is to set the function values of all equations to zero by selecting a value of x that also satisfies all constraints. This problem is known as constrained root solving, or multivariable root solving when the dimension of x is greater than 1.
Note a SCNLE is created in a similar way as a SNLE problem. It is recommened you complete reading the SNLE section before reading the remainder of the section.
Example 1: Bounded SNLE
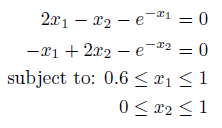
To setup this problem, it can be entered as follows:
nleq = @(x) [ 2*x(1) - x(2) - exp(-x(1));
-x(1) + 2*x(2) - exp(-x(2))];
% Bounds
lb = [0.6;0];
ub = [1;1];
% Starting Guess
x0 = [-5;5];
And the problem solved by passing the problem variables to OPTI, and calling solve on the resulting object:
Opt = opti('nleq',nleq,'bounds',lb,ub,'x0',x0)
% Solve the SCNLE problem
[x,fval,exitflag,info] = solve(Opt)