Quadratic Programming Overview
As detailed in the MPC overview the optimization problem that is to be solved at each sample is formulated as a Quadratic Programming (QP) Problem. This page gives a very brief overview of what a QP is within the MPC context and this toolbox.
Standard jMPC QP Problem
The QP solved by the jMPC Toolbox takes the following form:
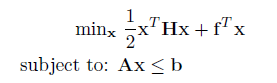
where:
| H | Quadratic (diagonal) and bilinear (off-diagonal) cost function terms | Dense Matrix, Symmetric |
| f | Linear cost function terms | Dense Vector |
| A | Linear inequality constraint terms | Dense Matrix |
| b | Linear inequality constraint right hand side | Dense Vector |
| x | Decision variables | Dense Vector |
For the purposes of this documentation the decision variable vector x is renamed to z to avoid conflicting with the state variable vector common in control.
QP Example
In order to solve the QP at each sample within an MPC simulation, the jMPC Toolbox provides several QP Solvers, which all solve the problem as defined above. As an example of using one of the supplied solvers, consider the following (toy) example:

All supplied solvers use the same calling strategy, as follows:
[z,exitflag,iter] = qpsolver(H,f,A,b,maxiter,tol,verbose,z0,lam0,t0)
Where the arguments are as follows:
H | Cost function H matrix |
f | Cost function f vector |
A | Constraint function A matrix |
b | Constraint function b vector |
maxiter | Maximum number of iterations of the solver (optional) |
tol | Convergence tolerance (scalar, optional) |
verbose | 0 for no print out, 1 for print out (optional) |
z0 | Initial (warm start) decision variable vector (optional) |
lam0 | Initial (warm start) dual variable vector (optional) |
t0 | Initial (warm start) slack variable vector (optional) |
And the return variables are:
z | Solution vector |
exitflag | Flag indicating solver status (1 = solved, negative = failed) |
iter | Number of iterations taken to solve |
The above problem can be solved using quad_wright, one of the supplied solvers with jMPC:
H = eye(3);
f = [-2;-3;-1];
A = [1 1 1;3 -2 -3; 1 -3 2];
b = [1;1;1];
%Setup Solver
maxiter = 30;
tol = 1e-6;
verbose = 1;
%Solve
[z,exitflag,iter] = quad_wright(H,f,A,b,maxiter,tol,verbose)
See the QP Solvers page for more information on the supplied solvers and their algorithms.