jNL
Create a Nonlinear Model object.
Syntax
jNLobj = jNL(xfnc,C)
jNLobj = jNL(xfnc,C,param)
jNLobj = jNL(xfnc,C,param,x0)
jNLobj = jNL(xfnc,yfnc,param,x0)
Description
jNLobj = jNL(xfnc,C) creates the jNL object with the nonlinear state function specified as a function handle, xfnc. C is a matrix (n_out x states) which relates the model's internal states to it's output.
jNLobj = jNL(xfnc,C,param) specifies additional parameters to be passed to the nonlinear state function xfnc. These must be a cell array such as:
param = {l,m,n};
jNLobj = jNL(xfnc,C,param,x0) specifies the initial states of the nonlinear model. When this argument is omitted, the initial states are assumed to be all zero.
jNLobj = jNL(xfnc,yfnc,param,x0) uses a second function handle to point to a nonlinear function to relate model states to outputs. You must supply x0 when using a nonlinear output function.
Nonlinear Functions
This class will only correctly simulate continuous nonlinear functions (ODEs) which are written in standard Cauchy form. This means higher order equations must be re-written as a collection of first order equations, which is the norm when using an ODE solver in MATLAB.
It is also important to note that due to the way this class is simulated, your nonlinear model must be time invariant. This means that your Ordinary Differential Equation (ODE) must not be a function of time (t), only a function of states and input. For example:
xdot(1,1) = x(2);
xdot(1,2) = param{1}*sin(u);
Noting that t is used only as a placeholder so that the function can be called by the ODE solver, and is not used within the differential equation.
Example
Given the following set of differential equations, which describe a helicopter model [4], create a jNL object for use in a MPC Simulation:
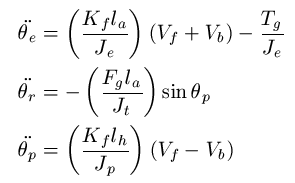
First create a new m file called nl_heli.m:
% Nonlinear Helicopter Model
%Assign Parameters
[Je,la,Kf,Fg,Tg,Jp,lh,Jt] = param{:};
xdot(1,1) = x(2);
xdot(2,1) = (Kf*la/Je)*(u(1)+u(2))-Tg/Je;
xdot(3,1) = x(4);
xdot(4,1) = -(Fg*la/Jt)*sin(x(5));
xdot(5,1) = x(6);
xdot(6,1) = (Kf*lh/Jp)*(u(1)-u(2));
end
Second, to create the jNL object, assuming the parameters and C matrix have already been declared as variables:
param = {Je,la,Kf,Fg,Tg,Jp,lh,Jt};
Plant = jNL(@nl_heli,C,param);
See the 3DOF Helicopter Case Study and CSTR Case Study for use of this class.